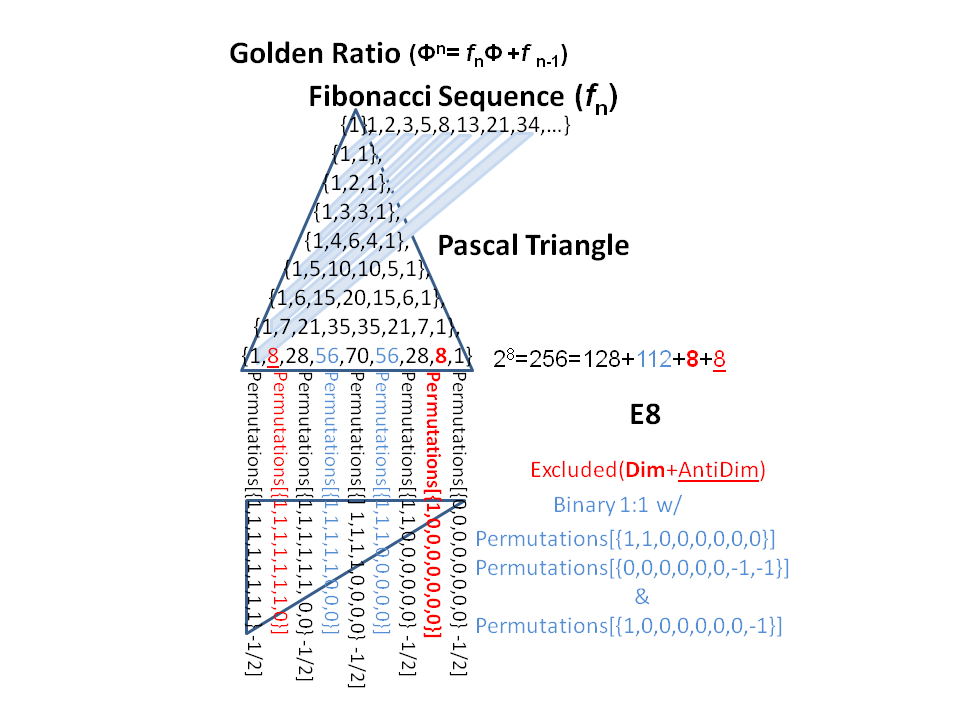
Fibonacci Triangle Pattern

Fibonacci Triangle Pattern - Web using right triangles, pythagorean theorem a^2 + b^2 = c^2, and a few supplies, you will learn to construct a fibonacci spiral. In the fibonacci series, each digit equals the sum of the two integers before it. Web different ways in java to print a fibonacci triangle. We can also derive the sequence in pascal’s triangle from the fibonacci sequence. Web the fp markets pattern pulse is a dedicated weekly release that features emerging technical patterns and structure to be aware of across key markets. But let’s explore this sequence a little further. Web patterns in the fibonacci numbers. Web c# program to generate fibonacci triangle. Here, the middle numbers of each row are the sum of the two numbers above it. The next diagonal has the counting numbers (1,2,3, etc).

J++) { int next = first_value + second_value; But let’s explore this sequence a little further. 1, 3, 21 and 55. Here, the middle numbers of each row are the sum of the two numbers above it. Printf(the right triangle of fibonacci series numbers pattern\n); (the fourth diagonal, not highlighted, has the tetrahedral numbers.) symmetrical. The triangle is also symmetrical. Web c# program to generate fibonacci triangle. Web fibonacci numbers start with 1, 1 and then you find the next term by adding the previous two. Web this python program prints the right angled triangle of numbers in the fibonacci series pattern using a while loop.

More Fibonacci / Pascal Triangle Patterns Visualizing a Theory of

This pattern turned out to have an interest and importance far beyond what its creator imagined. But let’s explore this sequence a little further. The fibonacci numbers occur as the sums of binomial coefficients in the shallow diagonals of pascal's triangle: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987,. The first diagonal.

More Fibonacci / Pascal Triangle Patterns Visualizing a Theory of

Web c++ program to generate fibonacci triangle. It is a number triangle that starts with 1 at the top, and each row has 1 at its two ends. Here are some patterns people have already noticed in the final digits of the fibonacci numbers: So we get 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89. The fibonacci.

Elliott Wave Patterns & Fibonacci Relationships Core Reference Guide

{ int first_value = 0; The triangle is also symmetrical. The next diagonal has the counting numbers (1,2,3, etc). But what makes this sequence so special and interesting? For (int j = 1;

Concepts Fibonacci Patterns

We already know that you get the next term in the sequence by adding the two terms before it. Asked 7 years, 9 months ago. It is a number triangle that starts with 1 at the top, and each row has 1 at its two ends. (the fourth diagonal, not highlighted, has the tetrahedral numbers.) symmetrical. Here, the middle numbers.

Magic behind the Fibonacci sequence Chalkdust

J++) { int next = first_value + second_value; Is there a pattern in the final digits? Let's see the c++ example to generate fibonacci triangle. This area of interest also happens to coincide with the 50% fibonacci retracement level, so the confluence could attract crude oil bears and allow the selloff to resume. However, i am trying in this way.

Pascal's Triangle Definition, History, Patterns and its Correlations

In this program, we are getting input from the user for the limit for fibonacci triangle, and printing the fibonacci series for the given number of times (limit). Web patterns within the triangle. So we get 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89. The fibonacci sequence exhibits a certain numerical pattern which originated as the answer.

Figure 2 from A Novel Fibonacci Pattern in Pascal's Triangle Semantic

But let’s explore this sequence a little further. Here, the middle numbers of each row are the sum of the two numbers above it. In the fibonacci series, each digit equals the sum of the two integers before it. Here are some patterns people have already noticed in the final digits of the fibonacci numbers: We already know that you.

A Pascal's Triangle Fibonacci Sequence Mapping Download Scientific

The next diagonal has the counting numbers (1,2,3, etc). We can also derive the sequence in pascal’s triangle from the fibonacci sequence. Web the fp markets pattern pulse is a dedicated weekly release that features emerging technical patterns and structure to be aware of across key markets. The fibonacci sequence exhibits a certain numerical pattern which originated as the answer.

Numbers Magick World Mysteries Blog

Printf(the right triangle of fibonacci series numbers pattern\n); The first diagonal is, of course, just 1s. Web patterns within the triangle. In this program, we are getting input from the user for the limit for fibonacci triangle, and printing the fibonacci series for the given number of times (limit). (161.8% fibonacci extension) to 1.3830 (38.2% fibonacci extension) region opens up.

Elliott Wave Patterns & Fibonacci Relationships Core Reference Guide

Let's see the c# example to generate fibonacci triangle. With seed values f 1 = 1 and f 2 = 1. Web pascal’s triangle contains the fibonacci sequence, which is an infinite sequence of numbers that are generated by adding the two previous terms in the sequence. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,.…. In.

= = ⌊ ⌋ ().

The fibonacci sequence exhibits a certain numerical pattern which originated as the answer to an exercise in the first ever high school algebra text. For (int j = 1; Web how to generate a right angle fibonacci series pyramid in java? In this program, we are getting input from the user for the limit for fibonacci triangle, and printing the fibonacci series for the given number of times (limit).

Here Are Some Patterns People Have Already Noticed In The Final Digits Of The Fibonacci Numbers:

This one differs from the typical square, but it is elegant and simple. Here, for reference, is the fibonacci sequence: We already know that you get the next term in the sequence by adding the two terms before it. This pattern turned out to have an interest and importance far beyond what its creator imagined.

Web Triangle Chart Patterns.

Web this python program prints the right angled triangle of numbers in the fibonacci series pattern using a while loop. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987,. But what makes this sequence so special and interesting? { int first_value = 0;

Web Patterns In The Fibonacci Numbers.

Web c# program to generate fibonacci triangle. In this program, we are getting input from the user for the limit for fibonacci triangle, and printing the fibonacci series for the given number of times (limit). Web fibonacci sequence in pascal’s triangle. (161.8% fibonacci extension) to 1.3830 (38.2% fibonacci extension) region opens up the april high (1.3846) but usd/cad may face range bound conditions as it no longer trades.